Considere a figura abaixo, onde imaginamos que o ângulo de vértice A é sempre reto, muito embora o ponto C esteja se deslocando na perpendicular ao segmento .

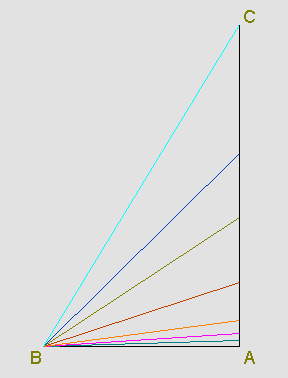
Dado o triângulo ABC, retângulo em A, 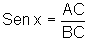, onde x é a medida em graus do ângulo de vértice B.

Conforme x varia no intervalo ]0,90[, podemos observar que o quociente, entre as medidas de AC e BC, varia no intervalo aberto que vai de 0 até 1.
De fato, quando a medida do ângulo de vértice B é pequena, próxima de zero, o cateto oposto AC é pequeno, com medida próxima de zero.
Por outro lado, conforme a medida do ângulo de vértice B aumenta, tendendo a 90^o, o comprimento do cateto AC aumenta e, também, o da hipotenusa BC. No limite, com o ângulo de vértice em A sendo reto e fixo, o ângulo de vértice B tendendo a ser reto, o ângulo de vértice C tende a ser nulo e o quociente 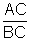tende a 1.

Assim, a imagem da função Sen é ]0,1[.

No caso da função Cosseno a análise é semelhante, porém contrária.
Dado o triângulo ABC, retângulo em A, Cos x = 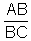, onde x é a medida em graus do ângulo de vértice B.

Conforme x varia no intervalo ]0,90[, podemos observar que o quociente entre as medidas, do cateto adjacente AB e a hipotenusa BC, varia no intervalo aberto que vai de 0 até 1.
De fato, conforme a medida do ângulo B se aproxima de 0^o, os comprimentos AB e BC tendem cada vez mais a se tornarem iguais: conseqüentemente, o quociente 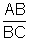tende a 1.

Por outro lado, quando a medida do ângulo B se aproxima de 90^o, o comprimento BC será muito grande, cada vez maior, tendendo a infinito. Dessa maneira, o quociente 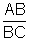tende a 0.

Assim a imagem da função Cos é ]0,1[.

Para a função Tangente, novamente fazemos uma análise semelhante.
Dado um triângulo ABC, retângulo em A, Tg x = 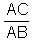, onde x é a medida em graus do ângulo de vértice B.

Conforme x varia no intervalo ]0,90[, podemos observar que o quociente entre as medidas, do cateto oposto AC e do cateto adjacente AB, varia no intervalo aberto que vai de 0 até infinito.
De fato, quando a medida do ângulo B está muito próxima de 0^o, AC é muito pequeno, enquanto AB está fixo. Portanto o quociente 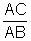tende a 0.

Entretanto, quando a medida do ângulo B está muito próxima de 90^o, AC é muito grande, cada vez maior, tendendo a infinito, e AB está fixo. Logo o quociente 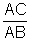tende a infinito.

Assim a imagem da função Tg é 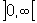.