Para construir o hexágono regular inscrito numa dada circunferência, precisamos ter claro que, sendo um polígono de 6 lados, todos de igual medida, dividimos o ângulo de 360° em 6 partes, portanto cada uma com 60°.
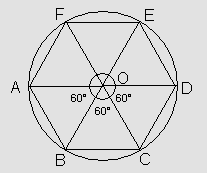
Obtemos assim 6 pontos na circunferência: A, B, C, D, E e F.
Examinemos o triângulo
ABO. Esse triângulo é isósceles pois 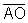 e
e 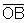 têm
ambos medida igual ao raio r da circunferência. Como o ângulo
têm
ambos medida igual ao raio r da circunferência. Como o ângulo
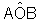 mede
60°, os ângulos da base do triângulo somam 120° e,
como são congruentes, medem ambos 60°.
mede
60°, os ângulos da base do triângulo somam 120° e,
como são congruentes, medem ambos 60°.
Assim o triângulo
ABO é eqüilátero e, portanto, 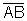 também mede r. Como isso pode ser observado em cada um dos
seis triângulos, que são todos congruentes,
concluímos que AB=BC=CD=DE=EF=FA=r.
E, finalmente,
também mede r. Como isso pode ser observado em cada um dos
seis triângulos, que são todos congruentes,
concluímos que AB=BC=CD=DE=EF=FA=r.
E, finalmente, 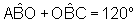 ,
por exemplo. Assim,
,
por exemplo. Assim, 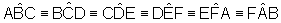 e cada um mede
120°.
e cada um mede
120°.
Uma observação
adicional pode ser feita: o quadrilátero ABCO é um losango,
pois seus quatro lados são todos congruentes e tem medida igual
a r.
