Dado o número real x, seja Q=P(x) e seja R=P .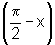

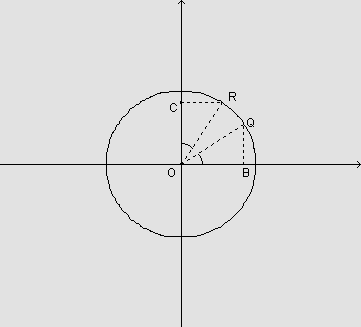
Na figura, observamos que os triângulos OBQ e OCR são congruentes pelo caso LAA_o, pois:

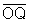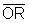• e são congruentes porque são ambos raios da circunferência;
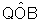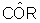• os ângulos e são congruentes pois medem ambos x radianos.
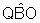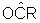• os ângulos e são congruentes pois são ambos retos.

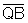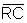Logo, os lados e são congruentes, bem como, 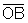e .

Portanto, sen x=cos 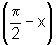e cos x= sen .

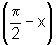Da definição de tangente de um arco, podemos escrever:

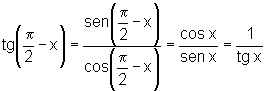
Pela interpretação geométrica da tangente de um arco,

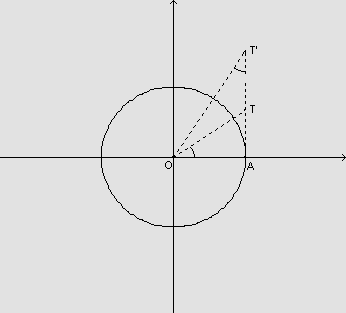
Geometricamente, na figura, observemos no triângulo OAT: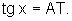

Também observemos o triângulo OAT': temos que a medida d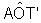e é 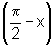radianos e a medida de é x radianos, pois são ângulos complementares de um triângulo retângulo.

Temos que 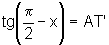e, por outro lado

,

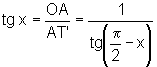de onde, concluímos que 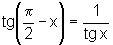.