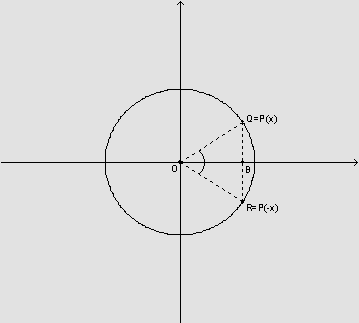
Dado o número real x, seja Q=P(x) e seja R=P(-x).

Na figura, observamos que os triângulos OBQ e OBR são congruentes pelo caso LAL, pois:

• têm um lado comum, ;
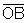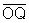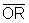• e são congruentes porque ambos são raios da circunferência;
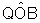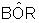• os ângulos e são congruentes pois medem ambos x radianos.

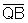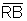Logo, os lados e são congruentes e, portanto, sen(-x)= -sen x, pois são opostos no plano cartesiano, em relação ao eixo horizontal.

Também cos(-x)=cos x, pois 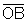é lado comum de triângulos congruentes.

Da definição de tangente de um arco, podemos escrever:

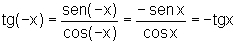
Pela interpretação geométrica da tangente de um arco,

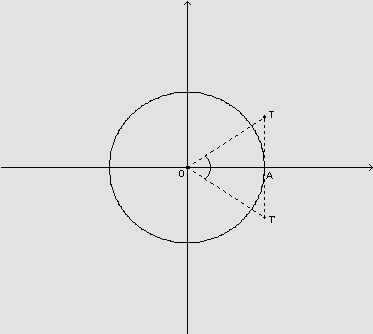
Geometricamente, na figura, observamos que os triângulos OAT e OAT' são congruentes pelo caso ALA, pois:

• têm um lado comum;
• cada um tem um ângulo reto;
• cada um tem um ângulo de medida x radianos.

Logo, os segmentos 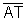e são congruentes e, portanto, tg(-x)=-tg x, pois são opostos no plano cartesiano, em relação ao eixo horizontal.