Utilizando apenas os fatos:
i) cos(-x)=cos x e sen(-x)=-sen(x)
e
ii) sen 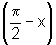 =cos x e cos
=cos x e cos
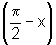 =sen x
=sen x
podemos provar várias outras propriedades:
iii) sen 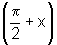 =cos
x e cos
=cos
x e cos 

Geometricamente, observamos que os triângulos OBP e OCQ são
congruentes pelo caso LAAo, pois ambos têm um lado que
é raio, um ângulo reto e um ângulo de medida x radianos.
Logo 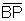 e
e 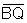 são congruentes, bem como
são congruentes, bem como 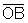 e
e  . Para estabelecer
a conclusão, basta observar o sinal que é dado pelo referencial
cartesiano.
. Para estabelecer
a conclusão, basta observar o sinal que é dado pelo referencial
cartesiano.
Também podemos
provar utilizando apenas argumentos que se baseiam no fato que 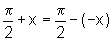 e nas propriedades i) e ii). Vejamos:
e nas propriedades i) e ii). Vejamos:
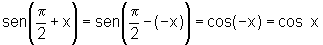
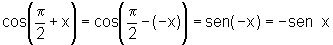
iv) 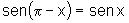 e
e 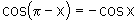
Geometricamente, observamos que os triângulos OBP e OCQ são
congruentes pelo caso LAAo, pois ambos têm um lado que
é raio, um ângulo reto e um ângulo de medida x radianos.
Logo 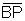 e
e 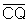 são congruentes, bem como
são congruentes, bem como 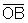 e
e  . Para estabelecer
a conclusão, basta novamente observar o sinal que é dado
pelo referencial cartesiano.
. Para estabelecer
a conclusão, basta novamente observar o sinal que é dado
pelo referencial cartesiano.
Também podemos
provar utilizando apenas argumentos que se baseiam no fato que 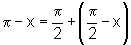 e nas propriedades i), ii) e iii). Vejamos:
e nas propriedades i), ii) e iii). Vejamos:
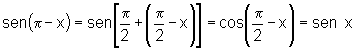
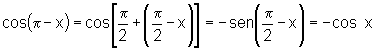
v) 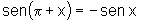 e
e 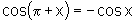
Geometricamente, observamos
que os triângulos OBP e OCQ são congruentes pelo caso LAAo,
pois ambos têm um lado que é raio, um ângulo reto e
um ângulo de medida x radianos. Logo 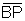 e
e 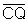 são congruentes,
bem como
são congruentes,
bem como 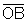 e
e  .
Para estabelecer a conclusão, basta novamente observar o sinal
que é dado pelo referencial cartesiano.
.
Para estabelecer a conclusão, basta novamente observar o sinal
que é dado pelo referencial cartesiano.
Também podemos
provar utilizando apenas argumentos que se baseiam no fato que 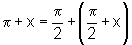 e na propriedade iii). Vejamos:
e na propriedade iii). Vejamos:
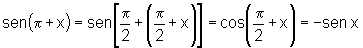
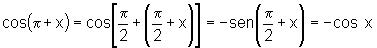
vi) 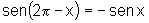 e
e 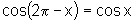
Geometricamente, observamos
que os triângulos OBP e OBQ são congruentes pelo caso LAAo,
pois ambos têm um lado que é raio, um ângulo reto e
um ângulo de medida x radianos. Logo 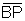 e
são congruentes, bem como
e
são congruentes, bem como 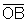 é lado comum. Para estabelecer a conclusão, basta novamente
observar o sinal que é dado pelo referencial cartesiano.
é lado comum. Para estabelecer a conclusão, basta novamente
observar o sinal que é dado pelo referencial cartesiano.
Também podemos
provar utilizando apenas argumentos que se baseiam no fato que 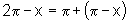 e nas propriedades iv) e v). Vejamos:
e nas propriedades iv) e v). Vejamos:
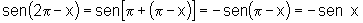
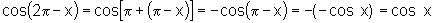
vii) 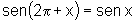 e
e 
Nesse caso não
há o que fazer pois os arcos x e 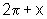 diferem por uma volta inteira e, portanto têm o mesmo seno e o mesmo
cosseno.
diferem por uma volta inteira e, portanto têm o mesmo seno e o mesmo
cosseno.
De modo geral 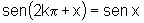 e
e 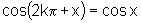 ,
para todo número inteiro k, pois os arcos x e
,
para todo número inteiro k, pois os arcos x e 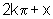 diferem
por um número inteiro de voltas e, portanto têm o mesmo seno
e o mesmo cosseno.
diferem
por um número inteiro de voltas e, portanto têm o mesmo seno
e o mesmo cosseno.
