1. Em primeiro lugar vamos interpretar geometricamente a relação: .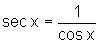

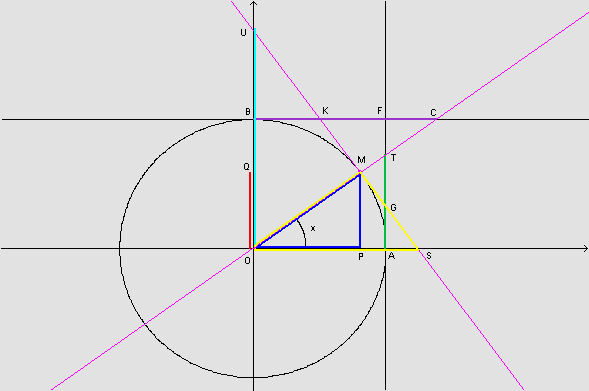
Na figura, os triângulos OMS e OPM são semelhantes, pois cada um deles tem um ângulo reto e um ângulo de medida x radianos; conseqüentemente, os terceiros ângulos são congruentes.

Assim, os lados homólogos são proporcionais e, portanto, ,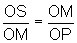
ou seja, .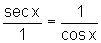

Portanto .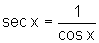

2. Em segundo lugar vamos interpretar geometricamente a relação: .

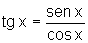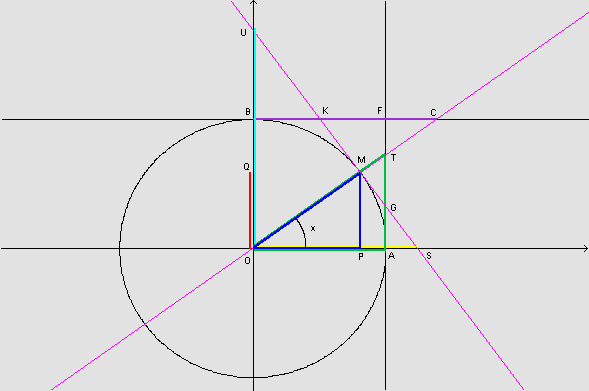
Observando, novamente, a figura, temos que os triângulos OAT e OPM são semelhantes, pois têm os ângulos internos respectivamente congruentes.

Dessa forma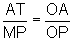

ou seja,

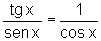
Portanto .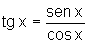

Podemos também mostrar que SM=tg x e que OT=sec x.

Isso é uma conseqüência imediata uma vez que os triângulos OAT e OMS são congruentes, pelo caso ALA: ambos têm um ângulo reto, um ângulo que mede x radianos e o lado compreendido entre esses ângulos que é raio da circunferência.

3. Em terceiro lugar vamos interpretar geometricamente a relação: .

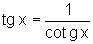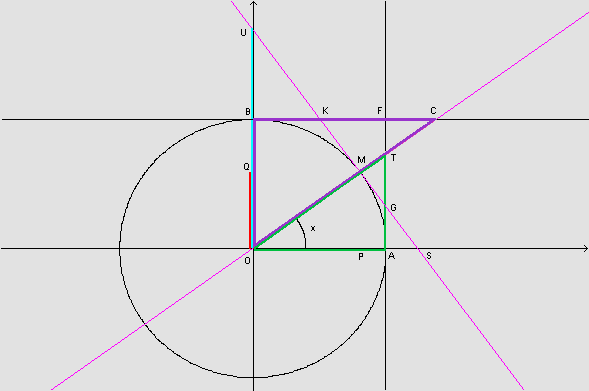
Os triângulos OAT e OBC são semelhantes, pois têm os ângulos internos respectivamente congruentes.

Dessa maneira, temos:

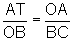
ou seja,

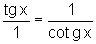
Portanto,

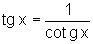
Podemos também mostrar que UM=cotg x.

Isso é uma conseqüência imediata uma vez que os triângulos OBC e OMU são congruentes, pelo caso ALA: ambos têm um ângulo reto, um ângulo que é o complementar daquele que tem x radianos e um lado que é raio da circunferência.

4. Em quarto lugar vamos interpretar geometricamente a relação: .

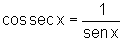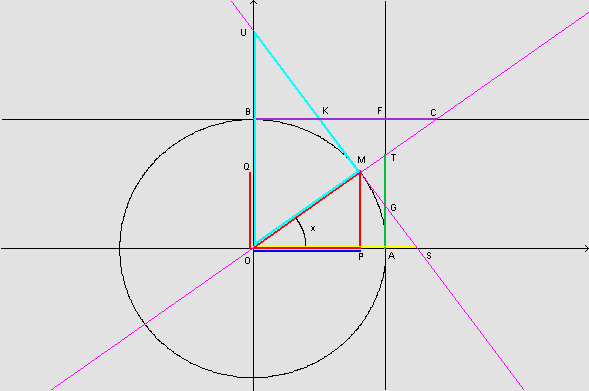
Os triângulos OPM e OMU são semelhantes, pois têm os ângulos internos respectivamente congruentes.

Dessa maneira, temos:

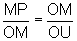
ou seja,

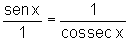
Portanto

Podemos também mostrar que OC=cossec x.

O que é uma conseqüência imediata uma vez que os triângulos OBC e OMU são congruentes, pelo caso ALA: ambos têm um ângulo reto, um ângulo que é o complementar daquele que tem x radianos e um lado que é raio da circunferência.