cotg2x+1=cossec2x
Prova Geométrica
Observando o triângulo BOC, pelo Teorema de Pitágoras, sabemos que:
BC2+OB2=OC2 (1)

Como BC=cotg x, OB=1
e OC=cossec
x, substituindo na relação (1), temos:
cotg2x+1=cossec2x.
Prova Algébrica
Sabemos que 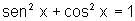 .
.
A relação a ser demonstrada só vale para 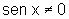 ,
caso contrário, não existem cotg x e cossec x.
,
caso contrário, não existem cotg x e cossec x.
Dessa forma, podemos dividir cada parcela por 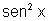 :
:
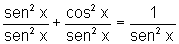 , ou
, ou
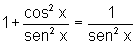
Mas 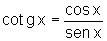 ,
e
,
e 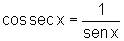
Portanto:
cotg2x+1=cossec2x.
