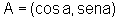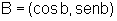A figura abaixo mostra a circunferência orientada de raio unitário e dois pontos e . Vamos calcular a distância entre esses dois pontos de duas maneiras: usando a "fórmula" da distância e a lei dos cossenos, provando assim a identidade: .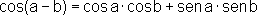

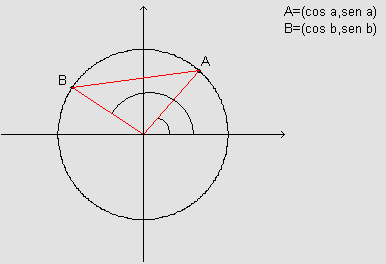
Usando a fórmula da distância, temos:

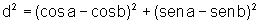(1)

e, usando a lei dos cossenos, temos:

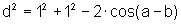, (2)

pois cos(a-b)=cos[-(b-a)]=cos(b-a) uma vez que cos é uma função par.

Igualando (1) e (2), temos:

.

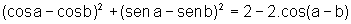Desenvolvendo os quadrados, fazendo as simplificações possíveis e utilizando a relação fundamental, temos:

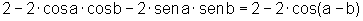
ou seja,

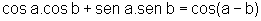
ou, equivalentemente,

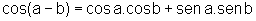
Podemos também provar que, no triângulo retângulo, vale:

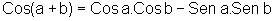
onde 0<a+b<180.