![]()
Primeiramente, observemos que ![]() representa
uma volta inteira na circunferência trigonométrica,
ou seja, dado o número real
representa
uma volta inteira na circunferência trigonométrica,
ou seja, dado o número real ![]() ,
fica determinado o ponto P(
,
fica determinado o ponto P(![]() )=A=(1,0)
que é a origem dos arcos.
)=A=(1,0)
que é a origem dos arcos.
Em segundo lugar, como k é um número inteiro, o
número 2k![]() =k.
=k.![]() ,
representa o número k de voltas dadas na circunferência.
Dessa maneira, para cada k inteiro, o número 2k
,
representa o número k de voltas dadas na circunferência.
Dessa maneira, para cada k inteiro, o número 2k![]() determina o ponto P(2k
determina o ponto P(2k![]() )=A=(1,0).
)=A=(1,0).
Sendo assim, os números x e x+2k![]() , embora diferentes, têm a mesma representação na
circunferência trigonométrica.
, embora diferentes, têm a mesma representação na
circunferência trigonométrica.
Portanto, ![]() ,
e
,
e ![]() ,
ou seja, as duas funções sen e cos são periódicas,
de período
,
ou seja, as duas funções sen e cos são periódicas,
de período ![]() .
.
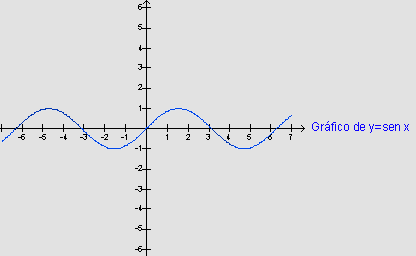
Para esboçar o gráfico
de y=sen x, observamos que para 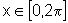 ,
temos:
,
temos:
-
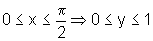 e, nesse
intervalo, a função é estritamente crescente, ou
seja, conforme x aumenta, y aumenta;
e, nesse
intervalo, a função é estritamente crescente, ou
seja, conforme x aumenta, y aumenta; 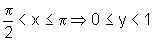 e, nesse intervalo,
a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;
e, nesse intervalo,
a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;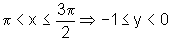 e, nesse intervalo,
a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;
e, nesse intervalo,
a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;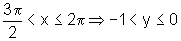 e, nesse intervalo,
a função é estritamente crescente, ou seja, conforme
x aumenta, y aumenta.
e, nesse intervalo,
a função é estritamente crescente, ou seja, conforme
x aumenta, y aumenta.
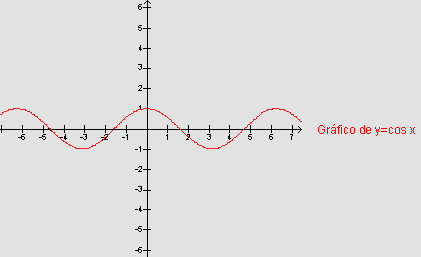
Para esboçar o gráfico
de y=cos x, observamos que para 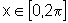 ,
temos:
,
temos:
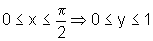 e, nesse intervalo,
a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;
e, nesse intervalo,
a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;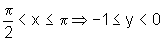 e, nesse intervalo,
a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;
e, nesse intervalo,
a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;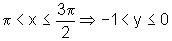 e, nesse intervalo,
a função é estritamente crescente, ou seja, conforme
x aumenta, y aumenta;
e, nesse intervalo,
a função é estritamente crescente, ou seja, conforme
x aumenta, y aumenta; e, nesse intervalo,
a função é estritamente crescente, ou seja, conforme
x aumenta, y aumenta.
e, nesse intervalo,
a função é estritamente crescente, ou seja, conforme
x aumenta, y aumenta.