Teorema de Pitágoras:

Dado um triângulo retângulo de catetos a e b e hipotenusa c, temos: a²+b²=c², isto é, a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

Existem muitas provas do Teorema de Pitágoras. Uma delas é a que segue abaixo.

Observemos a figura:

Trata-se de um quadrado de lados a+b, no qual está inscrito outro quadrado de lado c.

A área do quadrado maior é (a+b)². Mas essa área é igual à área do quadrado menor somada às áreas dos triângulos. Observe que todos os triângulos são congruentes, por LLL. Por isso suas áreas são iguais a .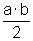

Então, (a+b)² =c²+4 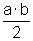, ou a²+2ab+b²=c²+2ab.

Simplificando a expressão, obtemos a²+b²=c².