Temos:

Definição: .

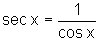Logo, o domínio da função secante é .

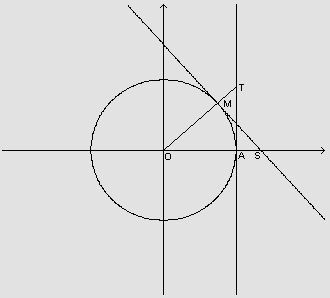
Também, a partir da circunferência trigonométrica, já sabemos que, na figura abaixo, para cada , sec x é a medida algébrica do segmento OS ou do segmento OT.

Da figura, observamos também que, para todo , , 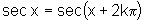onde k é um número inteiro qualquer. Assim a função sec é periódica, de período .

A fim de esboçar o gráfico de y=sec x, façamos a análise de como é a variação de y conforme x varia:

• e, nesse intervalo, a função é estritamente crescente, ou seja, conforme x aumenta, y aumenta;
• e, nesse intervalo, a função é estritamente crescente, ou seja, conforme x aumenta, y aumenta;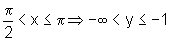
• e, nesse intervalo, a função é estritamente decrescente, ou seja, conforme x aumenta, y diminui;
• e, nesse intervalo, a função é estritamente decrescente, ou seja, conforme x aumenta, y diminui.

Observemos que as retas verticais de equação 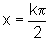, para k inteiro, não nulo, são assíntotas ao gráfico da função.

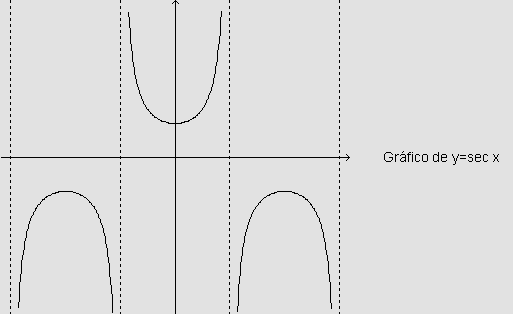
A função y=sec x tem como imagem o intervalo . Ela é uma função não limitada e periódica, de período .