![]() Observemos,
por exemplo, o gráfico de y=sen 2x
em comparação ao gráfico de y=sen x.
Observemos,
por exemplo, o gráfico de y=sen 2x
em comparação ao gráfico de y=sen x.
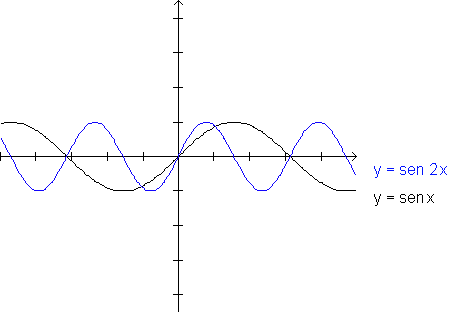
Aquilo que imediatamente chama a atenção é o fato de que o período de y=sen 2x é justamente a metade daquele de y=sen x.
Por outro lado, podemos examinar o gráfico de y=sen
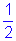 x em
comparação ao gráfico de y=sen x.
x em
comparação ao gráfico de y=sen x.
Neste caso, aquilo que imediatamente chama a atenção é
o fato de que o período de y=sen 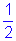 x
é justamente o dobro daquele de y=sen x.
x
é justamente o dobro daquele de y=sen x.
De modo geral, para b>0, a ação do coeficiente b
- até aqui considerado um número positivo - é a de
provocar mudança no período da função: enquanto
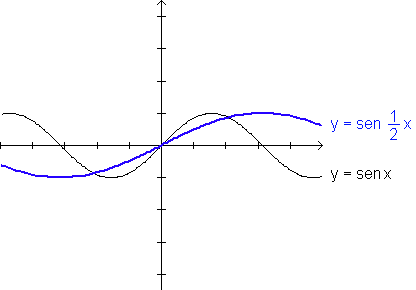
y=sen x é uma função de período ![]() ,
y=sen bx é uma função de período
,
y=sen bx é uma função de período 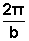 .
.
Entretanto ainda é preciso analisar o que acontece quando b é negativo; para isto basta observar que a função seno é uma função ímpar e, conseqüentemente, sen(-bx)=-sen(bx).
Dessa maneira, o gráfico de y=sen(-bx) é simétrico
em relação ao gráfico de y=sen bx, com relação
ao eixo horizontal.
