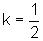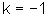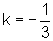Para responder a essa questão, façamos, por exemplo, k=1, k=2, , , ou qualquer outro valor para k e verifiquemos o que acontece.

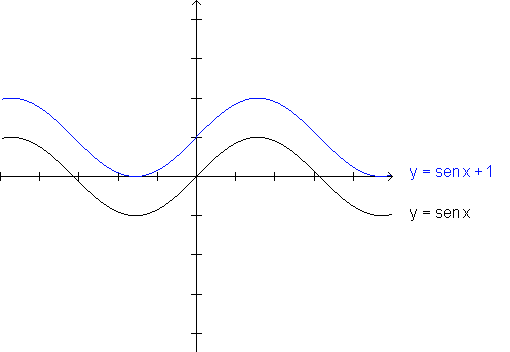
Observemos que cada ponto do gráfico de tem ordenada igual a uma unidade a mais do que a ordenada do ponto de mesma abscissa no gráfico de y=sen x. Ou seja, o gráfico de é o resultado de uma translação vertical de 1 unidade da curva que é gráfico de y= sen x.

Podemos facilmente generalizar esse raciocínio quando utilizamos outros valores de k, ou seja, a conclusão é análoga para qualquer outro valor de k: o gráfic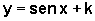o de sofre uma translação vertical de k unidades, quando comparado ao gráfico de 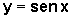. Portanto, o gráfico de "sobe" ou "desce" em relação à posição inicial de , conforme k>0 ou k<0 respectivamente.

Observação: É muito importante ter claro que y=sen x+k não é a mesma função que y=sen(x+k). Na primeira temos uma translação vertical de k unidades do gráfico de y=sen x, enquanto que na segunda temos uma translação horizontal. O uso dos parênteses é essencial no caso da segunda função.