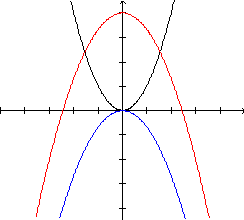
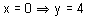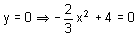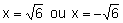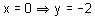Para desenhar 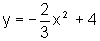, fazemos:

- em primeiro lugar, y=x²;

- em seguida, 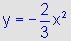, observando a reflexão em relação ao eixo horizontal do gráfico de ;

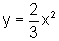- finalmente, 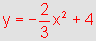é o resultado de uma translação vertical de 4 unidades do gráfico de .

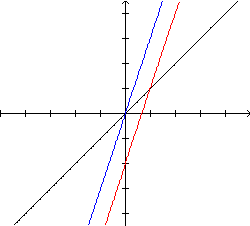
Para desenhar y=3x-2, fazemos:

- em primeiro lugar, y=x;

- em seguida, y=3x, observando a mudança de inclinação em relação ao gráfico anterior;

- finalmente, y=3x-2, como resultado de uma translação vertical de -2 unidades do gráfico anterior.

 

 

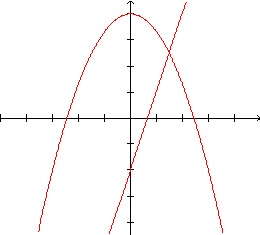
Colocando os gráficos das duas funções num mesmo par de eixos, isto é, "passando a limpo o que está nos interessando", temos:

 

Na primeira função temos: ou seja,

Na segunda função y=3x-2 temos:

 

Resolver a inequação dada 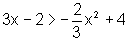reduz-se pois à resolução de uma equação - que permite encontrar os valores da abscissa x para os quais os gráficos se interceptam - e à leitura do gráfico. É preciso observar que nem sempre aparecem no gráfico os pontos de intersecção - como no gráfico desenhado, onde um dos pontos não aparece, devido à escala adotada - e, conseqüentemente, os cálculos algébricos são fundamentais.
Assim sendo:

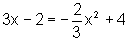
conduz a

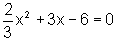
que, resolvendo a equação do segundo grau, nos fornece x=-6 ou .
Assim, a solução da inequação é o intervalo dado pela reunião de dois intervalos,

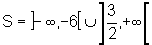
pois, para esses valores de x, o gráfico da função y=3x-2 se encontra acima do gráfico da função 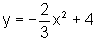.