![]()
Atribuindo valores ao coeficiente a, por exemplo ![]() ou
qualquer outro valor positivo, podemos verificar o que acontece. A seguir,
atribuindo valores negativos ao coeficiente a, por exemplo,
ou
qualquer outro valor positivo, podemos verificar o que acontece. A seguir,
atribuindo valores negativos ao coeficiente a, por exemplo, ![]() e
assim por diante, poderemos chegar a uma conclusão mais geral.
e
assim por diante, poderemos chegar a uma conclusão mais geral.
Em primeiro lugar, observamos que, a partir de y=x, construímos y=2x, considerando que cada ponto do seu gráfico tem ordenada igual ao dobro daquela do ponto de mesma abscissa no gráfico de y=x. Assim, y=2x tem por gráfico uma reta que tem inclinação igual ao dobro da inclinação de y=x.
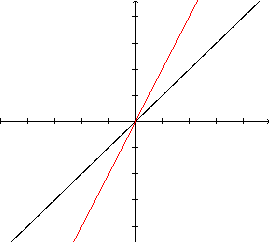
Se fizermos a=3, o gráfico de y=3x terá uma inclinação igual ao triplo da inclinação da reta que é o gráfico de y=x.
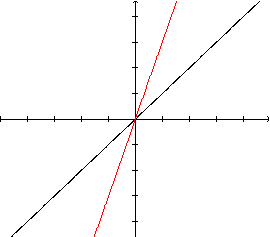
Se
fizermos ![]() ,
o gráfico de
,
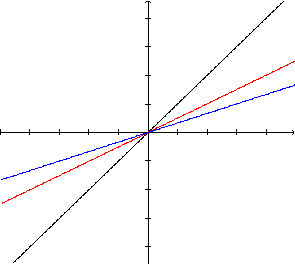
o gráfico de ![]() terá, respectivamente, uma inclinação igual à metade, ou à terça parte,
do valor da inclinação da reta que é o gráfico de y=x.
terá, respectivamente, uma inclinação igual à metade, ou à terça parte,
do valor da inclinação da reta que é o gráfico de y=x.
No caso de a ser negativo, observemos primeiro a situação mais simples de y=-x. Cada ponto desse gráfico tem ordenada igual ao oposto do valor da ordenada do ponto de mesma abscissa em y=x.
O seu gráfico é, portanto, uma reta simétrica em relação ao eixo horizontal à reta que é o gráfico de y=x. Também, evidentemente, é possível observar a simetria existente em relação ao eixo vertical.

Para outros valores negativos de a, podemos agora fazer os gráficos de maneira completamente análoga.
