Definição de parábola

Seja p um número real positivo.

Sejam dados um ponto F e uma reta r tais que 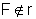e d(F,r)=2p. Consideremos o plano determinado por F e r, com um sistema de eixos cartesianos Oxy, de modo que o eixo x seja paralelo à reta r, o eixo y passe por F e a origem O seja eqüidistante de F e de r.

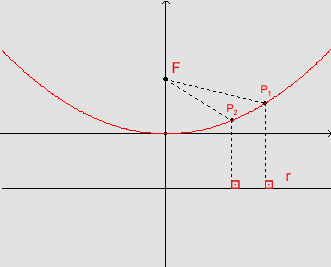
Vamos examinar o lugar geométrico dos pontos P=(x,y) do plano p tais que
d(P,F)=d(P,r).

Usando a distância entre dois pontos, temos:

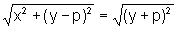
ou seja,

x²+y²-2py+p²=y²+2py+p²

e, portanto,

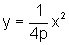
que é a equação do lugar geométrico procurado em sua forma mais simples.

Assim, podemos escrever a definição do lugar geométrico determinado pela equação que foi deduzida.

Definição:

Nas condições descritas acima, o lugar geométrico dos pontos P tais que
d(P,F)=d(P,r) é uma curva denominada parábola de foco F e diretriz r. A equação de uma parábola tal que a distância do foco à diretriz é 2p é dada por .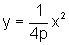

Observemos que y=x² é uma parábola, com 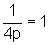ou seja 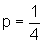e, portanto, seu foco está no ponto 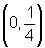e sua diretriz é a reta .

 

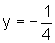Observações:

1. Escolhendo outro sistema de coordenadas, é claro que a equação da parábola muda. Nas figuras abaixo apresentamos outras situações.

a) quando a diretriz ainda é paralela ao eixo horizontal e o foco está no eixo vertical, mas s diretriz está acima do eixo horizontal e o foco abaixo:

Nesse caso a equação da curva é 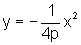, sendo F=(0,-p) e a diretriz é a reta y=p.

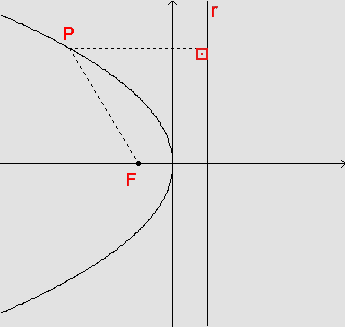
b) quando a diretriz é paralela ao eixo vertical e o foco está no eixo horizontal. Trocando as variáveis x e y, obtemos a equação 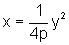que é uma parábola com foco no ponto (p,0) e diretriz a reta x = -p.

Se p>0, temos:

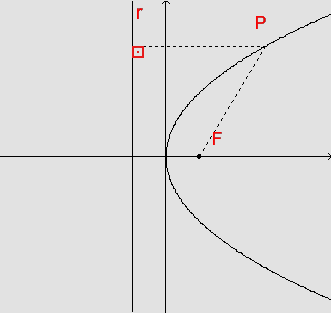
Se p<0, temos:

2. Observamos que toda parábola tem um vértice. Esse ponto é o ponto médio do segmento que liga o foco perpendicularmente à reta diretriz.