De fato,

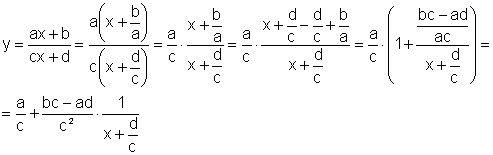
As operações realizadas só têm sentido se os parâmetros a, b, c e d obedecerem determinadas condições. De fato, quando colocamos a e c em evidência, precisamos ter .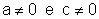

É preciso observar que:

· se a=0 e c=0, a função é constante, y= 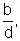e a análise é outra;

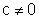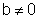· se a=0 e , com , temos a função y= 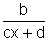, que é uma função do mesmo tipo, mais simples. Se b=0, temos y=0 e a análise é outra;

· o caso e c=0, com 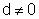e b qualquer, não precisa ser considerado, pois a função dada seria do primeiro grau, y=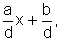 e a análise também seria outra.

Na função mais geral 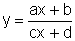, evidentemente, como já vimos, c não pode ser zero; também é preciso que 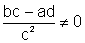pois, se assim não for, a função dada é uma função constante, 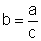o que não interessa na análise.

Observemos que bc-ad=0 engloba todos os casos que precisamos excluir. De fato,

· se a=b=0, a função dada é função nula;

· se c=d=0, não existe a função;

· se b=d=0, a função dada é constante e igual a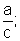

· se a=c=0, a função dada é constante e igual a ;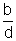

· se bc=ad, a função dada é constante e igual a .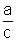

Assim sendo,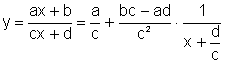
pode ser pensada como a função 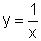sendo transladada horizontalmente para produzir a função 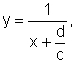que foi multiplicada pelo fator 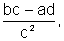constante havendo mudança de inclinação, para, em seguida, sofrer uma translação vertical através da constante 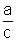.