![]()
Atribuindo valores ao coeficiente a, por
exemplo a=2, a=3, 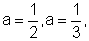 ou
qualquer outro valor positivo, podemos verificar o que acontece.
ou
qualquer outro valor positivo, podemos verificar o que acontece.
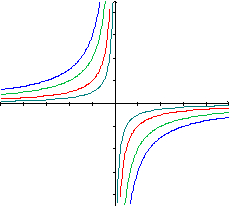
Para qualquer valor de a>0 o gráfico de
y= 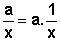 sofreu mudança
de inclinação em relação ao gráfico de y=
sofreu mudança
de inclinação em relação ao gráfico de y= 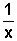 : quando a>1, o gráfico se afasta dos eixos; quando 0<a<1,
a curva se aproxima dos eixos.
: quando a>1, o gráfico se afasta dos eixos; quando 0<a<1,
a curva se aproxima dos eixos.
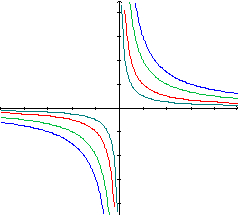
O gráfico de y= -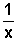 é o simétrico
em relação ao eixo x do gráfico de y=
é o simétrico
em relação ao eixo x do gráfico de y= 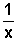 ,
pois para um mesmo valor de x, as ordenadas são opostas. Em seguida, conforme
variamos o parâmetro a, sendo a<-1, o gráfico de y=
,
pois para um mesmo valor de x, as ordenadas são opostas. Em seguida, conforme
variamos o parâmetro a, sendo a<-1, o gráfico de y=  se afasta do gráfico de y= -
se afasta do gráfico de y= -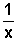 , ou seja se afasta dos eixos; se -1<a<0, a curva se aproxima dos
eixos. Conforme varia, observamos a
mudança de inclinação do gráfico em relação
ao gráfico da função inicial y=
, ou seja se afasta dos eixos; se -1<a<0, a curva se aproxima dos
eixos. Conforme varia, observamos a
mudança de inclinação do gráfico em relação
ao gráfico da função inicial y= 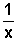 .
.
 |