![]()
Atribuindo diferentes valores,
por exemplo, k=2, k=3, k=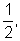 k=-1, k=-3, verificamos o que acontece, quando comparamos o gráfico obtido
com o gráfico inicial de
k=-1, k=-3, verificamos o que acontece, quando comparamos o gráfico obtido
com o gráfico inicial de  .
.
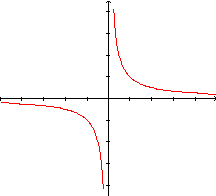
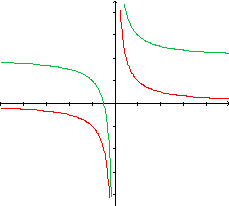
Observemos que cada ponto do gráfico de 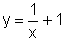 tem ordenada igual a uma unidade a mais do que a ordenada do ponto de
mesma abscissa no gráfico de
tem ordenada igual a uma unidade a mais do que a ordenada do ponto de
mesma abscissa no gráfico de 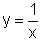 .
Ou seja, o gráfico de
.
Ou seja, o gráfico de 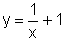 é uma hipérbole, que é
o resultado de uma translação vertical de 1 unidade do gráfico
de
é uma hipérbole, que é
o resultado de uma translação vertical de 1 unidade do gráfico
de 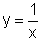 .
.
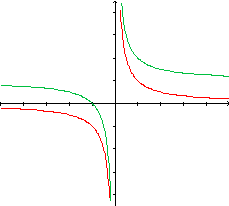
Um raciocínio análogo pode ser
realizado quando comparamos 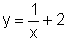 com
com 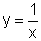 para concluir que
houve uma translação vertical
de 2 unidades no gráfico da nova função quando comparado ao da função
original.
para concluir que
houve uma translação vertical
de 2 unidades no gráfico da nova função quando comparado ao da função
original.
Para qualquer outro valor de k, a conclusão
é semelhante: o gráfico de 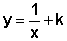 sofreu uma translação vertical de k unidades, quando comparado
ao gráfico de
sofreu uma translação vertical de k unidades, quando comparado
ao gráfico de 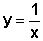 e, portanto,
para cada valor de k, é uma hipérbole que "subiu" ou "desceu" em relação
à posição inicial de
e, portanto,
para cada valor de k, é uma hipérbole que "subiu" ou "desceu" em relação
à posição inicial de  .
.
 |
