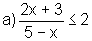
Sejam
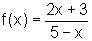e g(x)=2.
De imediato vemos que a função g é constante e igual a 2. Já a função
f pode ser colocada de maneira tal que fiquem visíveis as transformações
realizadas na função cujo gráfico é 
.
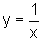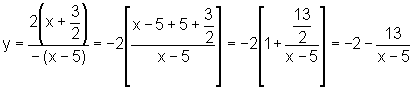
Então, o gráfico é obtido a partir de através das seguintes transformações:
- translação horizontal de 5 unidades;
- mudança de inclinação
provocada pelo fator 13;
- reflexão no eixo
x, para obtenção da função oposta;
- translação vertical de -2 unidades.
Traçando os gráficos de f e g num mesmo par de eixos, obtemos:
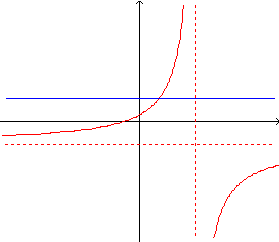
Queremos
resolver a inequação f(x)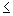
g(x),
ou seja, queremos descobrir para quais valores de x o gráfico de
f está abaixo do gráfico de g. Para isso, vamos calcular
o valor da abscissa x do ponto I de intersecção entre os gráficos
de f e g:
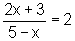
ou seja, multiplicando os dois termos da equação por 5-x,
2x+3=10-2x
e daí,
.
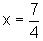Logo, a solução procurada para a inequação é:
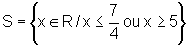
que, em notação de intervalos, pode ser escrita:
 |
 |
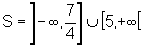