Como o eixo de simetria é vertical, temos que cada uma das curvas procuradas é o gráfico de uma função do segundo grau.

Como cada uma das curvas corta o eixo x nos pontos de abscissas m e n, temos que os números m e n são as raízes da função cujo gráfico é a referida parábola.

Assim sendo, temos que, na forma fatorada, podemos escrever

y=a(x-m).(x-n)

ou seja,

y=a[x²-(m+n).x+mn]

ou, completando os quadrados, temos

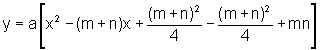
de onde

ou