
Como
a parábola tem vértice V=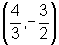 , a abscissa do foco é a mesma que a do vértice pois ambos estão no eixo
de simetria.
, a abscissa do foco é a mesma que a do vértice pois ambos estão no eixo
de simetria.
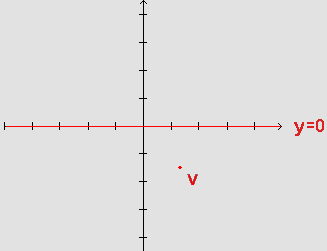
Como a ordenada do vértice é negativa, a ordenada do foco também o será e, sendo a diretriz o eixo x - ou seja a reta y=0 - a parábola tem concavidade voltada para baixo.
Como
a distância do vértice à reta diretriz é 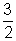 ,
a distância do vértice ao foco também deve ser, portanto a ordenada do
foco é 2.
,
a distância do vértice ao foco também deve ser, portanto a ordenada do
foco é 2. 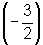 = -3.
= -3.
Logo
o foco é o ponto F= 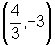
Seja X=(x,y) um ponto qualquer pertencente à parábola que queremos determinar. Seja P=(x,0) um ponto qualquer da diretriz. Temos então:
d(X,F)=d(X,P)
ou seja,
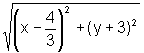 =
=
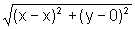
Elevando-se ao quadrado ambos os membros da igualdade, temos:
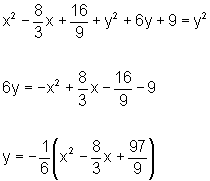
ou seja,
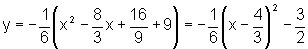
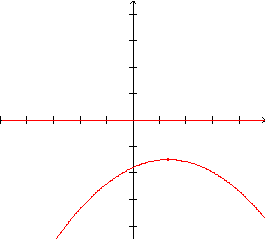
 |
