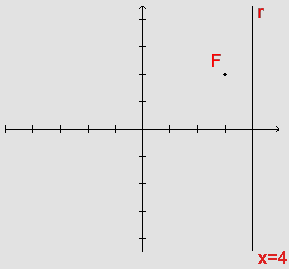
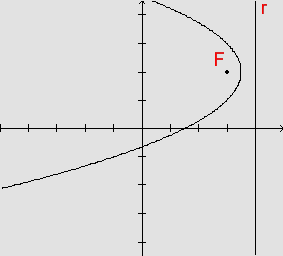
Temos F=(3,2); seja X=(x,y) um ponto qualquer da curva que estamos procurando e seja P=(4,y) um ponto qualquer da diretriz. Da definição de parábola como lugar geométrico dos pontos cuja distância ao foco é igual à distância até a diretriz, temos:

d(X,F)=d(X,P)

=

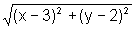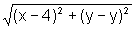
onde, elevando os dois membros da igualdade ao quadrado, obtemos:

x²-6x+9+y²-4y+4=x²-8x+16

ou seja,

2x=3-y²+4y

de onde

x=

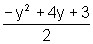
ou seja,

expressão obtida completando-se os quadrados. Finalmente:

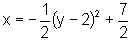que é a equação da parábola procurada.