Função bijetora
Uma
função 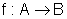 é dita
bijetora quando é simultaneamente injetora e sobrejetora.
é dita
bijetora quando é simultaneamente injetora e sobrejetora.
O
fato de f ser injetora significa que quaisquer dois diferentes
pontos do domínio A são levados em dois diferentes pontos da imagem Im
f  B. Equivalentemente,
podemos dizer que cada ponto da imagem é proveniente de um único ponto
do domínio.
B. Equivalentemente,
podemos dizer que cada ponto da imagem é proveniente de um único ponto
do domínio.
O fato de a função ser sobrejetora significa que a imagem coincide com o contra-domínio B, ou seja, para cada ponto b do conjunto B existe um ponto a do conjunto A que é levado por f em b, isto é f(a)=b.
Toda função estritamente crescente ou estritamente decrescente é injetora logo é bijetora sobre a imagem.
