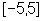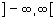Na figura temos o gráfico de uma função representada no intervalo . Supondo que o comportamento é o mesmo no intervalo , podemos estabelecer a expressão algébrica que define essa função.

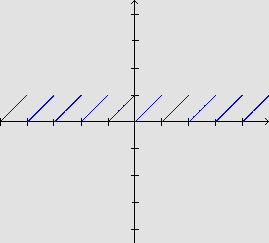
Observando com cuidado, percebemos que o gráfico dessa função é um conjunto de segmentos de reta que são paralelos. Um desses segmentos tem como extremidades os pontos (0,0) e (1,1). Daí, é fácil ver que esse segmento está contido na reta y=x. Considerando os segmentos paralelos a esse, temos:

• para :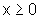

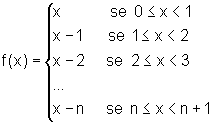
• para :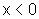

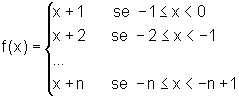
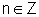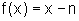Logo, o gráfico acima é o gráfico da função que, para cada , é dada por , tal que .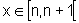

Esse exemplo nos apresenta a possibilidade de criar um sem número de outras funções periódicas de maneira análoga. Basta definir uma função num intervalo, por exemplo, [0,1] e, em seguida, nos intervalos sucessivos, realizar translações horizontais do gráfico da função que foi inicialmente definida.