Propriedade: Se f é uma função periódica
de período p, então n.p com 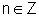 ,
também é um período para f.
,
também é um período para f.
Prova:
Vamos fazer a demonstração por indução finita, considerando, inicialmente n inteiro positivo.
Temos que se n=1,
a afirmação é verdadeira, 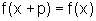 ,
para todo
,
para todo 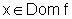 ,
pois por hipótese f é periódica de período
p.
,
pois por hipótese f é periódica de período
p.
Verifiquemos que se
a afirmação é válida para n=k, então
também o é para n=k+1.
Com efeito,
 .
.
Pelo princípio de indução finita, a propriedade é verdadeira para todo n inteiro positivo.
Como
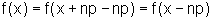
a propriedade vale
também para n negativo.
