a) f(x)=ln x2
O domínio de f é R-{0} e observamos que f(-x)=ln (-x)2, ou seja, f(x)=f(-x).
Logo, a função é par.
O gráfico é:
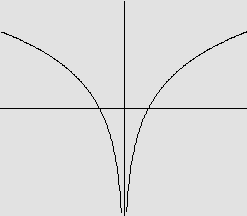
Observe que, para x>0, ln x2=2.ln x.
b) f(x)=sen x
O domínio de f é R e observamos que f(-x)=sen(-x)=-sen x, ou seja, f(x)=-f(-x).
Logo, a função é ímpar.
O gráfico é:
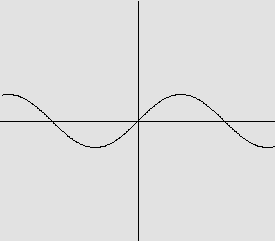
c) f(x)=cos x
O domínio de f é R e observamos que f(-x)=cos (-x), e como cos x=cos (-x),
então f(x)=f(-x). Logo, a função é par.
O gráfico é:
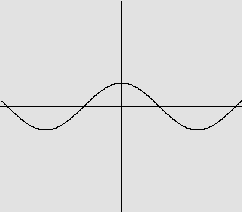
d) f(x)=x3+1 O domínio de f é R e observamos que
f(-x)=(-x)3+1, ou seja,
f(-x)=-x3+1. Logo, a função não é par nem ímpar.
O gráfico é:
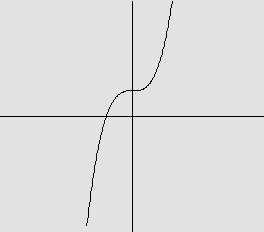
e) f(x)=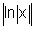 
O domínio de f é R-{0} e observamos que
f(-x)=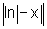
ou seja,
f(x)=f(-x). Logo, a função é par.
O gráfico é:
 |
 |
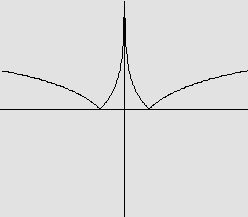