Decida se as funções abaixo, dadas por seus gráficos, são pares, ímpares, ou nenhuma delas:

a)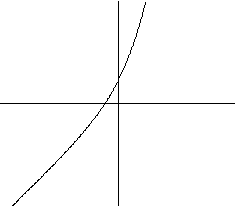

b)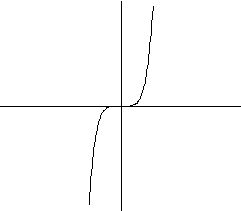

c)

d)

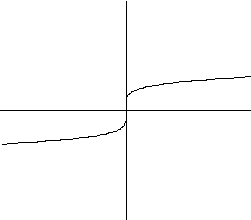
e)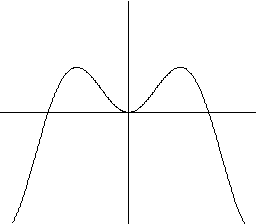

f)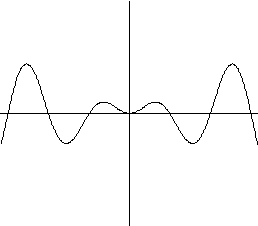

Esboce o gráfico das funções abaixo, decidindo antes sobre as eventuais características de cada uma delas quanto às possíveis simetrias em relação ao eixo vertical ou à origem.

a) f(x)=ln x²

b) f(x)=sen x

c) f(x)=cos x

d) f(x)=x³+1

e) f(x)=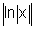

Um fato interessante é que uma função qualquer, não necessariamente par ou ímpar, sempre pode ser decomposta na soma de uma função par com uma ímpar! De fato, observe:

.

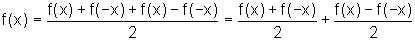a) Chamando g(x) e h(x), a primeira e a segunda parcelas, respectivamente, mostre que a função g é par e que a função h é ímpar.

b) Mostre também que se a função f dada inicialmente é par ou ímpar, então a função h ou g é nula, respectivamente.

c) Escreva f(x)=ln x como soma de duas funções: uma par e outra ímpar.

d) Faça o mesmo com f(x)= e^x.