Dada a função 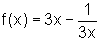, o seu domínio é Dom f=R-{0}.

i) A função f pode ser decomposta, por exemplo, em uma soma de duas funções , cujos domínios são:
Dom g=R e Dom h=R-{0}.

O gráfico de g₁ pode ser obtido, a partir de y=x, através de uma mudança de inclinação. O gráfico de h₁, por sua vez, é obtido a partir de , fazendo-se uma reflexão no eixo x e uma mudança de inclinação.

Traçando os dois gráficos num mesmo par de eixos, juntamente com o gráfico da função inicial, temos:

Várias análises podem ser realizadas ao examinar o gráfico da função f e é sempre interessante buscar a compreensão do comportamento de determinado gráfico.

ii) Uma outra maneira, dentre várias, de se decompor a função f é através de um quociente, ou sej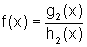a, . De fato, podemos reescrever a função f da seguinte maneira:

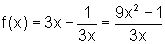
Assim temos g₂(x)=9x²-1, com Dom g₂=R e h₂(x)=3x com Dom h₂=R.

O gráfico da função g₂ é obtido, a partir de y=x², através de uma mudança de inclinação e de uma translação vertical de -1 unidade. O gráfico de h₂ é obtido, a partir de y=x, através de uma mudança de inclinação.

Traçando os dois gráficos num mesmo par de eixos, juntamente com o gráfico da função inicial, temos:

Novamente, poderíamos fazer uma análise semelhante à anterior, a fim de interpretar a função f como quociente de g₂ e h₂.