![]()
Dada a função f(x)=x²-5x+6, com Dom f=R, temos que f pode ser escrita como
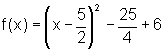
Logo
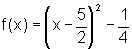
O gráfico de
f pode, portanto, ser obtido a partir de y=x2 fazendo
as transformações: translação horizontal de
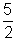 e translação
vertical de
e translação
vertical de 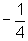 .
.
i) Uma das maneiras possíveis de se decompor f, por exemplo, como soma a de duas funções, f(x)=g1(x)+h1(x), é considerando
g1(x)=x2+6 e h1(x)=-5x
cujos domínios são Dom g1=R e Dom h1=R
O gráfico de g1 é obtido a partir de y=x2 através de uma translação vertical de 6 unidades. Já o gráfico de h1 é obtido, a partir de y=x, através de uma reflexão em relação ao eixo x e uma mudança de inclinação.
Traçando os dois gráficos num mesmo par de eixos, juntamente com o gráfico da função inicial, temos:
ii) Poderíamos
ter decomposto f como diferença de duas funções,
ou seja, 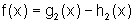 ,
com
,
com 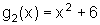 e
e 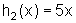 , cujos
domínios são ambos iguais a R.
, cujos
domínios são ambos iguais a R.
Traçando os dois gráficos num mesmo par de eixos, juntamente com o gráfico da função inicial, temos:
iii) Uma terceira forma possível é decompor f como produto de duas funções, ou seja, f(x)=g3(x).h3(x) é:
g3(x)=x-2 e h3(x)=x-3, cujos domínios são ambos iguais a R.
Os gráficos de g3 e de h3 são obtidos a partir de y=x através de uma translação vertical de -2 e -3 unidades, respectivamente.
Traçando os dois gráficos num mesmo par de eixos, juntamente com o gráfico da função inicial, temos:
 |
