a) Se 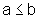, então .

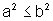A afirmação é falsa.
Contra-exemplo: -3<-2, mas (-3)² não é menor do que (-2)².

b) Se 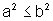, então .

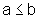A afirmação é falsa.
Contra-exemplo: (-3)²<(-4)², mas (-3) não é menor do que
(-4).

c) 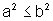é equivalente a .
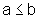Evidentemente, a afirmação é falsa devido aos itens anteriores.

d) 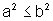é equivalente a .

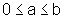Observemos que se 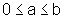, então .
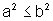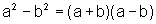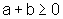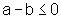De fato, como , temos que , porque ambos os números são não negativos, e , porque . Logo, 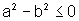e, portanto, .

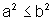Entretanto, a outra implicação, se 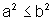então , é falsa.
Contra-exemplo: (-3)²<(-4)², mas (-3) não é menor do que
(-4), e ambos os números são negativos.

Logo, a equivalência proposta é falsa.

e) .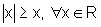
A afirmação é verdadeira. De fato, se 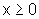, então .
Se x<0, então e portanto, . Logo, .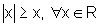

f) .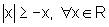
A afirmação é verdadeira. A demonstração é análoga à anterior, com um pequeno cuidado. Vejamos: se 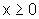, então , pois x é não negativo; se x<0, entã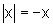o . Logo, .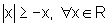

g) .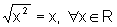
A afirmação é falsa.
Contra-exemplo: .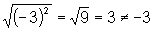

h) .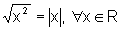
A afirmação é verdadeira e decorre da própria definição de raiz quadrada de um número não negativo: é um número não negativo, que elevado ao quadrado, produz o número dado inicialmente, ou seja, dado 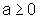, ,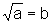 quando 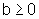e .
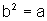