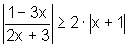
Sejam 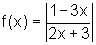e .
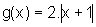Temos Dom f= 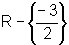e Dom g=R. Resolver a inequação proposta significa encontrar todos os valores reais de x, que são diferentes de 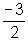e, para os quais, . Vamos observar o que ocorre graficamente.

i) O gráfico de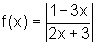

Inicialmente, temos:
= = = = =

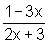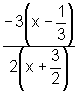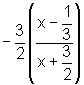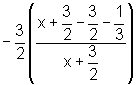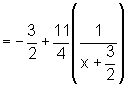
Logo,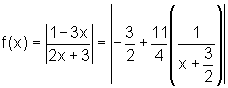

que pode ser escrita na forma

pois 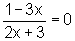quando 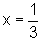, sendo que o quociente é positivo para 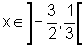e é negativo para .

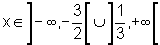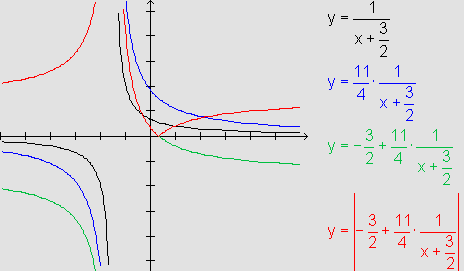
O gráfico de f pode ser obtido através de alguns gráficos auxiliares:

ii) O gráfico de g(x)=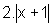

Temos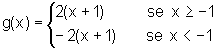

Pois x+1=0 quando x=-1.

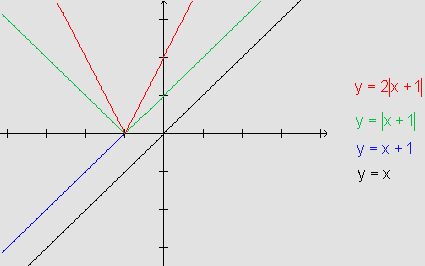
Assim, o gráfico de g pode ser obtido através de alguns gráficos auxiliares:

Finalmente, precisamos colocar os gráficos das duas funções num mesmo par de eixos.

Para tanto, observamos que:

• O primeiro gráfico provém de uma hipérbole que tem assíntota vertical em e assíntota horizontal em 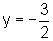. Além disso, as intersecções com os eixos ocorrem no ramo direito: quando x=0, 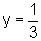e, quando y=0, coincidentemente, 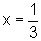. Dessa forma, conseguimos "passar a limpo" o gráfico, entendendo a ação do coeficiente 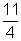. O outro ramo é desenhado levando em conta a simetria em relação ao centro da hipérbole: 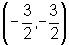. Finalmente, o gráfico de f é obtido através do rebatimento do trecho da curva que está abaixo do eixo horizontal e a manutenção do trecho que está acima.

• O segundo gráfico é mais simples, bastando considerar a reta y=2x+2, mantendo a parte acima do eixo x e rebatendo o trecho que está abaixo.

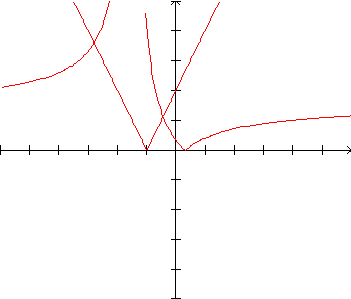
Para resolver a inequação, precisamos inicialmente encontrar as intersecções dos dois gráficos. No gráfico, observamos que:

• a "rebatida da reta" encontra a "rebatida da curva":
  
• a "original da reta" encontra a "original da curva":

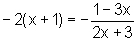
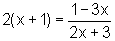
As duas situações nos levam à necessidade de resolver uma única equação:

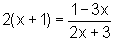
ou seja,

4x²+13x+5=0

e, portanto,

x=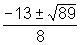
Portanto 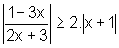quando .

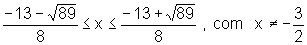Ou seja, o conjunto solução é

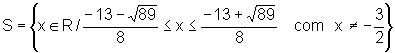
ou ainda,

.
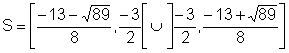