![]()
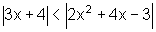
Sejam f(x)= 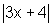 e g(x)=
e g(x)=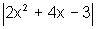 .
.
Temos Dom f=R e Dom g=R.
Resolver a inequação proposta significa encontrar todos
os valores reais de x para os quais f(x)<g(x).
Vamos observar o que ocorre graficamente:
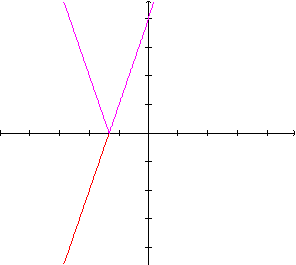
i) O gráfico
de f(x)= 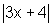
Temos: 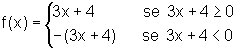
Como f(x)=0 quando
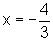 , podemos escrever
, podemos escrever
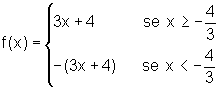
Logo, para construir
o gráfico de f,
- em segundo lugar,
o gráfico de y=f(x)=
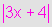
ii) O gráfico de 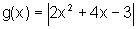
Temos 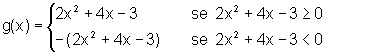
Como,
![]() =
=
= 2 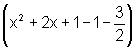 =
=
= 2 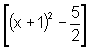 =
=
= ![]()
temos 2x2+4x-3=0
quando ![]() , ou seja,
, ou seja,
2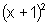 =5
=5
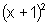 =
= 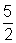
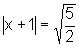 , isto é,
x+1=
, isto é,
x+1=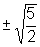 , ou
seja x=
, ou
seja x= 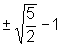
Portanto, g(x)= 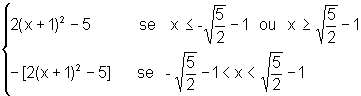
Para construir o gráfico de g fazemos:
- em primeiro lugar, o gráfico de y=2(x+1)2-5
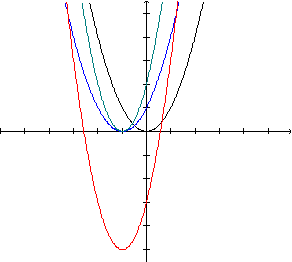
- em segundo lugar,
o gráfico de y=
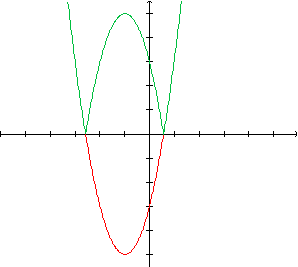
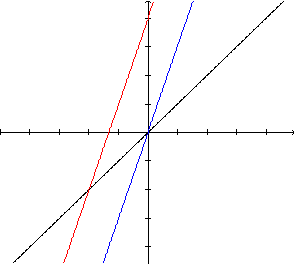
A fim de resolver a inequação proposta, precisamos comparar
os gráficos de f e g
e, para tanto, seus gráficos precisam estar no mesmo par de eixos.
Para copiar, o gráfico
de f, observamos que, quando x=0,
y=4 e quando y=0, 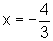 .
Obtemos assim, as intersecções da reta "original"
com os dois eixos e, pelo fato de se tratar de uma reta, essas informações
são suficientes. Fazer o rebatimento para obter o gráfico
de f é simples utilizando argumentos
de simetria.
.
Obtemos assim, as intersecções da reta "original"
com os dois eixos e, pelo fato de se tratar de uma reta, essas informações
são suficientes. Fazer o rebatimento para obter o gráfico
de f é simples utilizando argumentos
de simetria.
Para copiar o gráfico
de g, precisamos observar, inicialmente,
que a parábola "original" tem vértice no ponto
(-1,-5) e que suas raízes, isto é, os valores de x para
os quais y=0, são: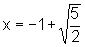 e
e 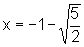 ; além
disso, a curva tem inclinação igual à da parábola
y=2x2. Essas informações devem ser suficientes
para a construção razoável da parábola "original"
que será utilizada para construir o gráfico de g.
Para tanto, utilizando argumentos de simetria, fazemos o "rebatimento"
da parte da curva que se encontra abaixo do eixo horizontal.
; além
disso, a curva tem inclinação igual à da parábola
y=2x2. Essas informações devem ser suficientes
para a construção razoável da parábola "original"
que será utilizada para construir o gráfico de g.
Para tanto, utilizando argumentos de simetria, fazemos o "rebatimento"
da parte da curva que se encontra abaixo do eixo horizontal.
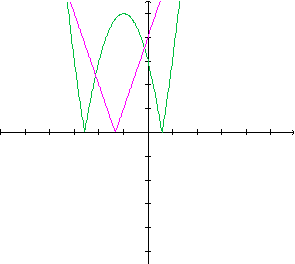
Observando os dois gráficos, temos intersecções, que não estão todas visíveis. Para encontrá-las, resolvemos as seguintes equações:
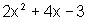 =
-(3x+4)
=
-(3x+4)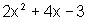 )=-(3x+4)
)=-(3x+4)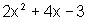 )=3x+4
)=3x+4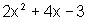 =3x+4
=3x+4 que se reduzem a duas apenas:
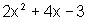 =
-(3x+4)
=
-(3x+4)e, portanto
2x2+7x+1=0
logo
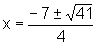
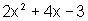 =3x+4
=3x+4
e, portanto
2x2+x-7=0
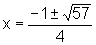
Encontramos assim quatro valores de x para os quais ocorre intersecção das duas curvas. Para ter uma noção razoável da correspondência entre os quatro valores de x que foram encontrados e os pontos onde ocorrem as intersecções entre as duas curvas, precisamos fazer uma estimativa:
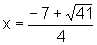 é um número que está no intervalo
é um número que está no intervalo 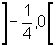 pois
pois 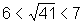 ;
;
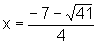 é um número que está no intervalo
é um número que está no intervalo 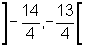 pois
pois 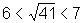 ;
;
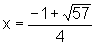 é um número que está no intervalo
é um número que está no intervalo 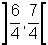 pois
pois 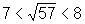 ;
;
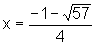 é
um número que está no intervalo
é
um número que está no intervalo 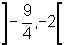 pois
pois 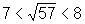 .
.
Com essas estimativas, podemos decidir o conjunto-solução da inequação, obtendo:
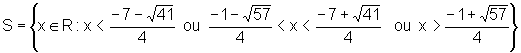
que também pode ser escrito em notação de intervalo:
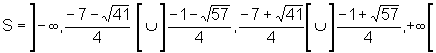 .
.
 |
