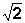é um número irracional

Suponhamos que 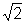seja um número racional.

Então devem existir inteiros a e b, não nulos, tais que:

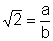
Podemos supor que a fração 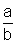é irredutível, isto é, que a e b são primos entre si.

Elevando ao quadrado os dois membros da igualdade, temos:

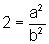
ou seja a²=2b² (*)
logo, a² é par e, portanto, a é par .

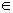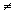Então, existe k Z, k 0, tal que a=2k; e substituindo em (*), temos:
(2k)²=2b²
ou seja, 4k² = 2b²
e, portanto 2k²=b²

ou seja, b² é par e, portanto, b também é par.

Logo, 2 é divisor comum de a e b.
Mas, a e b foram supostos primos entre si.

Portanto, assumindo que 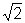é racional, chegamos a uma contradição, ou seja, a um absurdo.

Dessa maneira, mostramos que 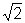não pode ser racional, isto é, é um número irracional.