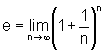Propriedade:
Sendo
dado o gráfico de 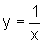 ,
vamos verificar que vale a seguinte propriedade:
,
vamos verificar que vale a seguinte propriedade:
Escolhendo
um número natural n e marcando no eixo das abscissas os pontos
correspondentes aos termos da progressão geométrica de primeiro termo
igual a 1 e razão 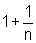 :
:
1,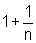 ,
, 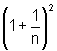 , ...,
, ..., 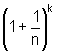 ,
...
,
...
teremos
que as áreas das regiões abaixo do gráfico de 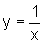 ,
determinadas em cada um dos intervalos
,
determinadas em cada um dos intervalos 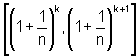 ,
são iguais.
,
são iguais.
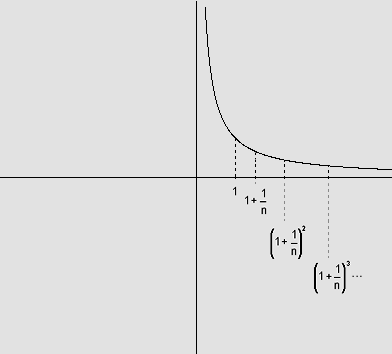
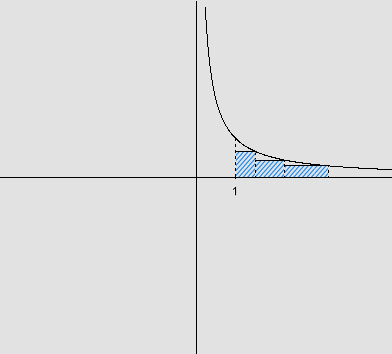
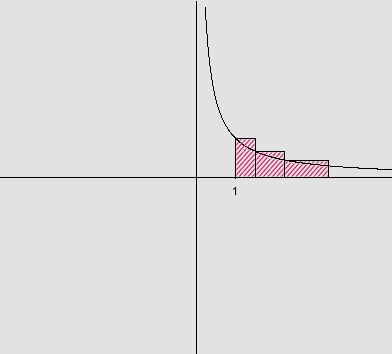
Consideremos r1, r2,..., rn e R1, R2,..., Rn os retângulos inscritos e circunscritos, conforme as figuras:
Então,
cada retângulo ri, para i variando de 1 a n, tem área
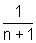 e cada retângulo
Ri , para i variando de 1 a n, tem área
e cada retângulo
Ri , para i variando de 1 a n, tem área
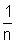 .
.
Assim,
chamando de A a área da região 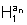 ,
temos que A está compreendida entre a soma das áreas dos retângulos inscritos
e a soma das áreas dos retângulos circunscritos, ou seja,
,
temos que A está compreendida entre a soma das áreas dos retângulos inscritos
e a soma das áreas dos retângulos circunscritos, ou seja,
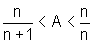

Fazendo
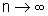 , pelo Teorema
do Confronto, temos
, pelo Teorema
do Confronto, temos 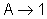 ,
,
isto
é, 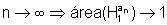
Como,
pela definição do número
e, área( 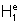 )=1,
podemos concluir que
)=1,
podemos concluir que
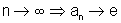
isto é, na notação mais precisa de limite temos que