O número e
Como a função ln é bijetora, dado o número real 1, existe um único real x, estritamente positivo, tal que ln x=1. Esse número, por definição, é o número e.
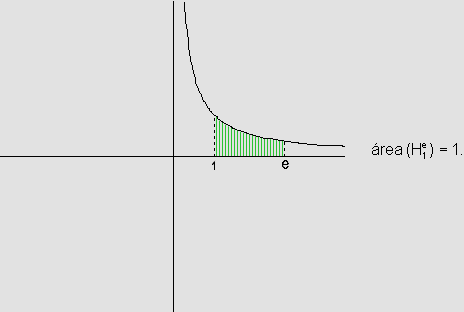
Assim,
e é o número tal que ln e=1, ou seja
é o número tal que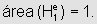 
Uma conseqüência imediata da definição é que e>1. Por
quê?
com x>0, observamos que a área da região, delimitada pelo eixo x, a curva e as retas x=1 e x=e, é maior do que zero, logo e>1.
Por outro lado, calculando
aproximadamente o número ln
3 através da soma das áreas dos retângulos inscritos em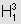 
,
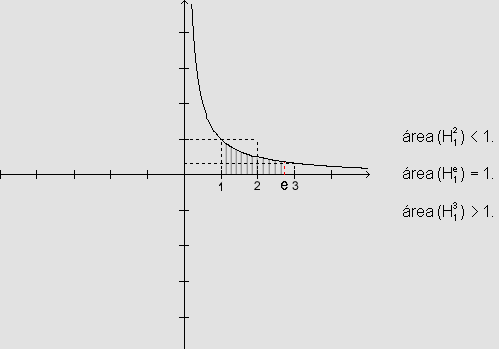
vemos que ln 3>1 e, portanto, e< 3.
É possível mostrar
também que a área
<1 para
concluir que e>2.
<1 pois essa região está inscrita num quadrado de lado
1.
O valor exato do
número e pode ser calculado através de uma propriedade
que Gregory
de St. Vincent observou em seu livro,
a respeito das áreas sob o gráfico da hipérbole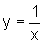 
,
com x>0. Em notação atual e precisa, envolvendo o conceito de limite,
definimos o número e como:
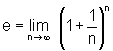
O número e é chamado base da função ln e a função ln é denominada função logarítmica de base e, sendo que, em homenagem a Napier, ln é também conhecido como o logaritmo natural ou logaritmo neperiano.
O número e também é conhecido como a constante de Euler.
Uma vez que a função ln é bijetora, ela é inversível. Podemos então considerar a sua inversa ln-1, que denominamos função exponencial, utilizando a notação
ln -1(x) = exp(x).
 |
 |