No caso de 0<a<1<b então pode acontecer que o produto ab seja maior ou menor que 1. De fato:
como
0<a<1 e b>0, temos ab<b;
e
de 1<b e a>0, temos a<ab.
Em qualquer caso, o produto ab está entre a e b, podendo ser maior ou menor que 1.
- Se 0<a<1<ab<b, então temos ab>1 e b>1. Então
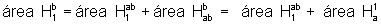
Logo
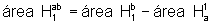
e, portanto, g(ab)=g(b)+g(a)=g(a)+g(b).
- Se 0<a<ab<1<b, então temos b>1. Então
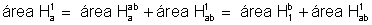
Logo
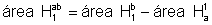
e, portanto, g(ab)=g(b)+g(a)=g(a)+g(b).
