![]()
Mudança
de base: para todos a e b estritamente positivos, sendo
b diferente de 1, temos: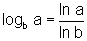 .
.
Observemos que o desenvolvimento realizado para introduzir os logaritmos nos levou a perceber que existe uma função logarítmica - ln - que é inversível e cuja inversa é a função exponencial - exp - definida para todo número real.
Dessa forma, podemos agora definir uma função exponencial generalizada, da seguinte maneira:
Assim,
na igualdade 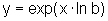 ,
tomando ln nos dois membros, temos:
,
tomando ln nos dois membros, temos:
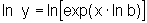
ou seja
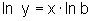 ,
pois a composta
,
pois a composta
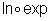 é a função identidade.
é a função identidade.
Então,
podemos escrever 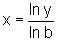 ,
que nos leva à definição da função inversa da exponencial geral
,
que nos leva à definição da função inversa da exponencial geral 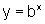 ,
colocando;
,
colocando;
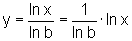 ,
que é denotada por
,
que é denotada por
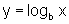 .
.
Assim,
temos: 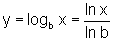
Seu
gráfico é obtido a partir do gráfico de y=ln x, através de uma mudança
de inclinação, provocada pelo fator 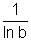 .
.
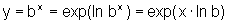 ,
,
