a) A equação da reta que passa por (a,f(a)) e (b,f(b)) é dada por:

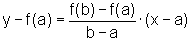
ou

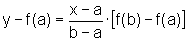
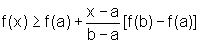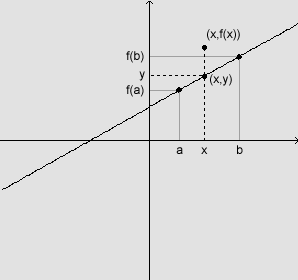
A desigualdade , para todo x pertencente ao intervalo [a,b], significa que os pontos do gráfico de f, que são da forma (x,f(x)) se encontram acima dos pontos (x,y) que estão na reta.

A sutileza está no fato de ser preciso observar que isso deve acontecer para todo x no intervalo [a,b], e para todos a e b no intervalo I.

b) Para mostrar que a função ln é côncava, basta mostrar que ela satisfaz a desigualdade mostrada no item a) para a função f.

No Exercício 6, item c), mostramos que 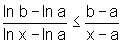, para quaisquer a, x, b, tais que .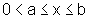

Assim, podemos escrever:

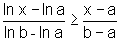
ou ainda, como 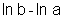>0,

de onde
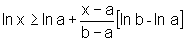, isto é, a função ln é côncava em seu domínio.