![]()
a)
A tese é mostrar que 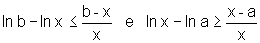
Para tanto, precisamos examinar vários casos:
i)
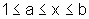
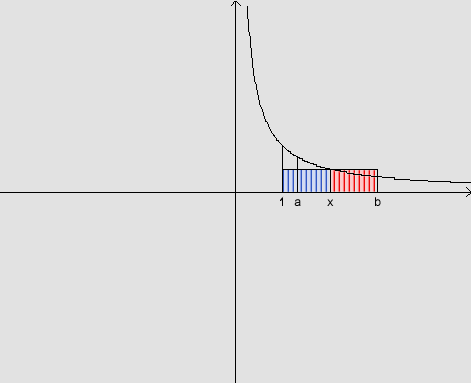
Observando
a figura, temos que 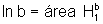 e
e 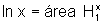 .
.
Portanto,
 que é a área
do retângulo "por fora".
que é a área
do retângulo "por fora".
Logo
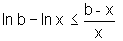 .
.
Por
outro lado, 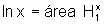 e
e 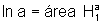 .
.
Portanto,
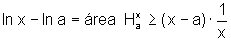 que é a área
do retângulo "por dentro".
que é a área
do retângulo "por dentro".
Logo
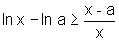 .
.
Assim, provamos as duas desigualdades na primeira situação.
ii)
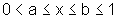
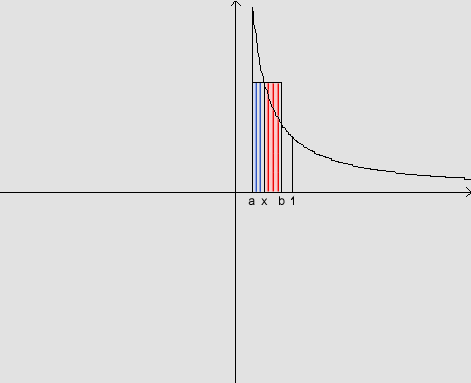
Observando
a figura, temos que 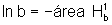 e
e 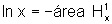 .
.
Portanto,
 que é a área
do retângulo "por fora".
que é a área
do retângulo "por fora".
Logo
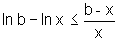 .
.
Por
outro lado, 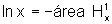 e
e 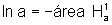 .
.
Portanto,
 que é a área
do retângulo "por dentro".
que é a área
do retângulo "por dentro".
Logo
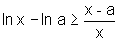 .
.
Assim, provamos as duas desigualdades na segunda situação.
iii)
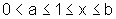
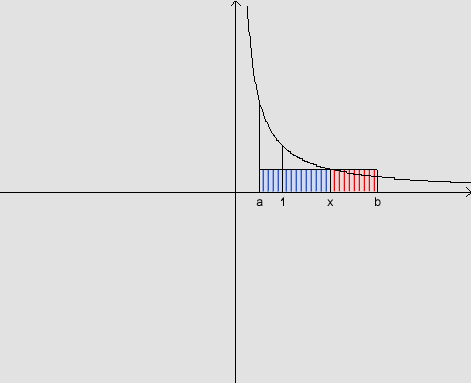
Observando
a figura, temos que 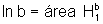 e
e 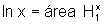 .
.
Portanto,
 que é a área
do retângulo "por fora".
que é a área
do retângulo "por fora".
Logo
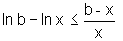 .
.
Por
outro lado, 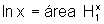 e
e 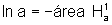 .
.
Portanto,
 que é a área
do retângulo "por dentro".
que é a área
do retângulo "por dentro".
Logo
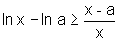 .
.
Assim, provamos as duas desigualdades na terceira situação.
iv)
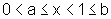

Observando
a figura, temos que 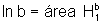 e
e 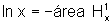 .
.
Portanto,  que é a área do retângulo "por fora".
que é a área do retângulo "por fora".
Logo
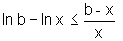 .
.
Por
outro lado, 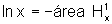 e
e 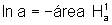 .
.
Portanto,
 que é a área
do retângulo "por dentro".
que é a área
do retângulo "por dentro".
Logo
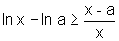 .
.
Assim, provamos as duas desigualdades na quarta situação.
Dessa
forma, temos que, se 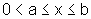 ,
então
,
então
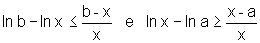 .
.
b)
Precisamos provar que, se 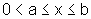 ,
então
,
então  .
.
Observamos,
em primeiro lugar, pelo item a), que lnx-lna>0
e 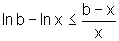 .
.
Assim, vamos dividir ambos os membros da desigualdade por lnx-lna:
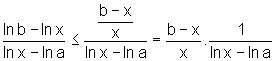 (A)
(A)
Também,
pelo item a) sabemos que 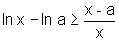 ,
logo, podemos tomar os inversos e temos:
,
logo, podemos tomar os inversos e temos:
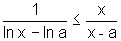 (B)
(B)
De
(A) e (B), podemos escrever 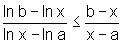 ,
como queríamos demonstrar.
,
como queríamos demonstrar.
c)
Finalmente, precisamos concluir que 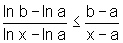 .
.
Observemos
que, de b), temos: 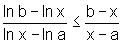 .
.
Mas,
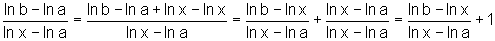
Logo,
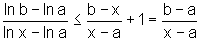 , ou seja,
, ou seja,
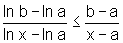 como queríamos demonstrar.
como queríamos demonstrar.
