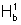![]()
a) Sabemos que ln 1 = 0. Logo, para todo a>0, podemos escrever:
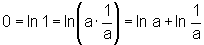 , pela propriedade do logaritmo do produto.
, pela propriedade do logaritmo do produto.
Assim,
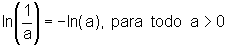 .
.
b)
Como 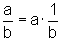 , para
todos a>0 e b>0, temos:
, para
todos a>0 e b>0, temos:
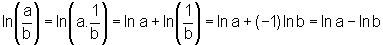 pela propriedade do logaritmo do produto e a propriedade demonstrada no
item a).
pela propriedade do logaritmo do produto e a propriedade demonstrada no
item a).
c) Temos an=a.a.a....a, então pelo Princípio da Indução Finita, podemos mostrar rigorosamente que, para todo a>0,
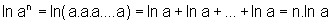 .
.
d)
Como 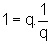 , para
todo q>0, podemos escrever:
, para
todo q>0, podemos escrever:
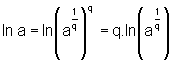 pela propriedade anterior.
pela propriedade anterior.
Logo
 .
.
e) Para todos p e q naturais, com q não nulo, e para todo a>0,
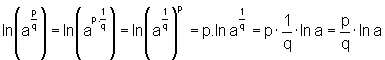
onde aplicamos a propriedade do item c) e depois a propriedade do item
d).
f) Como r é um número racional, podemos ter:
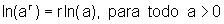 , é o mesmo que foi provado no item e).
, é o mesmo que foi provado no item e).
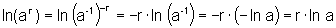 , onde
aplicamos o item anterior e, em seguida, o item a).
, onde
aplicamos o item anterior e, em seguida, o item a).
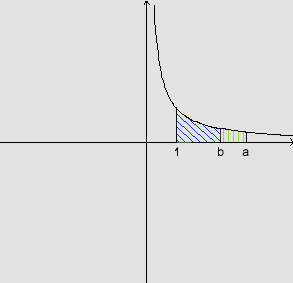
g) Para mostrar que ln é estritamente crescente, sendo a>0 e b>0, com a>b, precisamos considerar três casos:
i) a>b>1
a >
b > 1 : ln a > ln b > 0, pois área  e
e 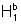
ii) a>1 e 0<b<1
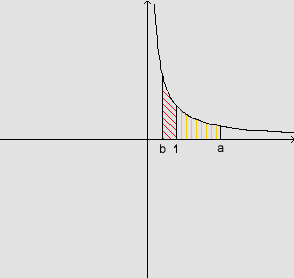
a >
1 e 0 < b < 1 : ln a > ln b, pois ln a =
área  > 0 e ln b = -área
> 0 e ln b = -área
 < 0
< 0
iii) 0<b<a<1:
0 <
b < a < 1 : ln a > ln b, pois ln a =
-área 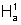 < 0 e ln b = -área
< 0 e ln b = -área 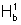 < 0. Da figura, área
< 0. Da figura, área 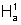 < área
< área 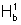 logo, -área
logo, -área 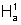 > -área
> -área