![]()
a) exp(a+b)=exp(a).exp(b)
Para provar a propriedade acima, sejam x=exp(a) e y=exp(b).
Então, tomando ln em ambos os lados das duas igualdades, temos: ln(x)=a e ln(y)=b.
e, portanto, a+b=ln x+ln y
ou seja, a+b=ln(x.y) por uma das propriedades dos logaritmos.
Tomando agora exp em ambos os membros da última igualdade, temos exp(a+b)=x.y , ou seja, exp(a+b)=exp(a).exp(b), como queríamos demonstrar.
b) exp(a-b)=exp(a):exp(b)
Para provar essa propriedade, sejam novamente, x=exp(a) e y=exp(b).
Então,
tomando ln em ambos os lados das duas igualdades, temos:
ln(x)=a e ln(y)=b.
e, portanto, a-b=ln x-ln
y
ou seja, a-b=ln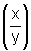 por uma das propriedades dos logaritmos.
por uma das propriedades dos logaritmos.
Tomando agora exp em ambos os membros da última igualdade, temos
exp(a-b)=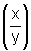 ,
ou seja, exp(a-b)=
,
ou seja, exp(a-b)=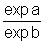 ,
como queríamos demonstrar.
,
como queríamos demonstrar.
