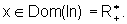a) Seja exp 1=A. Mas isso significa que ln A=1. Logo, da definição do número e, A=e. Portanto exp 1=e.
b)
ln(exp x)=x, uma vez que as funções ln e exp são inversas
uma da outra e então a composta
é a função identidade. É preciso observar que a igualdade ln(exp x)=x
vale para todo x real, pois 
c)
exp(ln x)=x pelo mesmo motivo. Entretanto, neste caso, a igualdade vale
para x>0, pois