![]()
Seja
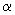 um número irracional
e a um número racional não nulo. Precisamos mostrar que
um número irracional
e a um número racional não nulo. Precisamos mostrar que 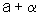 é um número irracional.
é um número irracional.
De
fato, suponhamos, por absurdo, que 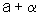 é racional. Então,
é racional. Então,
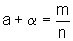 ,
com m e n inteiros e
,
com m e n inteiros e 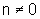 .
.
Mas,
nesse caso, temos 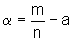 ,
ou seja
,
ou seja 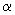 é a diferença
de dois racionais, logo é racional, o que é uma contradição.
é a diferença
de dois racionais, logo é racional, o que é uma contradição.
Logo
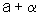 não é racional e,
portanto é irracional.
não é racional e,
portanto é irracional.
