Solução 1 - números irracionais

A fim de mostrar 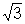que é um número irracional, procedemos de forma semelhante à que desenvolvemos para mostrar que 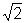é irracional.

Suponhamos então que 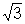seja um número racional.

Então existem inteiros 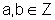, , 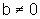tais que 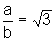. Mais ainda, podemos supor que a e b são primos entre si, ou seja a fração 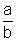não admite simplificação.

Com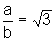o então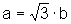
e, elevando ao quadrado os dois membros da igualdade, temos:

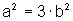
(*) ou seja, é múltiplo de 3.

Mas isso implica que a é múltiplo de 3, logo a=3.k, onde k é um número inteiro.

pois, do contrário, a seria da forma a=3k+1 ou a=3k₁+2, onde k e k₁ são números inteiros. Nesse caso, a²=9k²+6k+1 ou a²=9k₁² +12k₁+4, e, em qualquer caso, a² não seria múltiplo de 3

Substituindo em (*), temos:

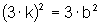ou seja, 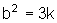² e, conseqüentemente, temos que b é múltiplo de 3.

Assim, concluímos que a e b têm 3 como um divisor comum, diferente de 1.

Portanto, assumindo que 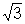é racional, chegamos a uma contradição, ou seja, a um absurdo.

Logo 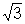é um número racional.