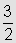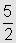Consideremos a partição do intervalo [1,3] dada pelos pontos: 1, , 2, , 3.

i) Vamos calcular a área aproximada por falta:

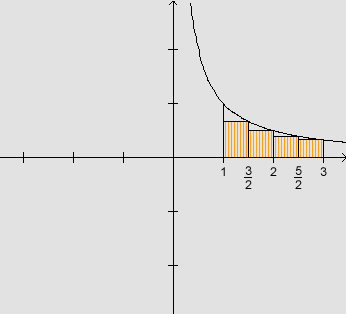
Chamando de s a soma das áreas dos 4 retângulos inscritos, temos:

ii) Vamos calcular a área aproximada por excesso:

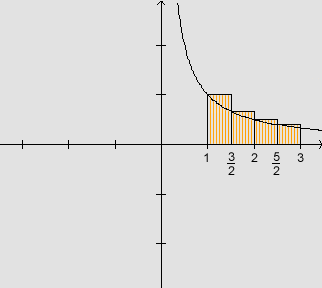
Chamando de S a soma das áreas dos 4 retângulos circunscritos, temos:

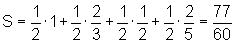
Assim,