ln(x-5)+1>ln(7-x)²-1

Observemos, em primeiro lugar, que a inequação só tem sentido para x>5 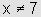e , pois, o domínio de f(x)=ln(x-5)+1 é 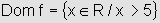e o domínio de g(x)=ln(7-x)²-1 é .

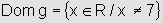Examinando o gráfico de f e g, temos:

onde o gráfico de f foi obtido, a partir de y=ln x, através de uma translação horizontal de 5 unidades, seguida de uma translação vertical de 1 unidade. O gráfico de g é uma translação vertical de -1 unidade do gráfico transladado de 7 unidades do logaritmo cujo logaritmando é o quadrado do argumento x.

A fim de resolver a inequação, precisamos primeiramente encontrar os pontos onde as duas curvas se interceptam, ou seja encontrar os valores de x - nesse caso, são dois - para os quais f(x)=g(x).

ln(x-5)+1=ln(7-x)²-1

Assim,

ln(x-5)=ln(7-x)²-2

Logo,

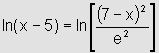
ou ainda,

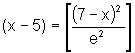
e²(x-5)=(7-x)²

e, portanto,

x²-(14+e²)x+49+5e²=0

de onde, obtemos:

isto é,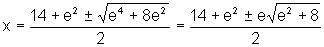

A solução da inequação é, portanto:

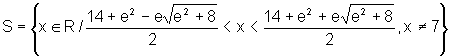
ou seja,
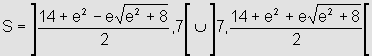