De fato, observando o gráfico de ,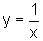

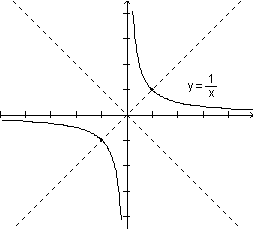
e girando-o de um ângulo de 45^o no sentido horário, obtemos o seguinte:

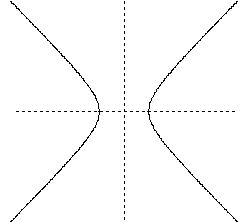
que nos permite estabelecer a conjectura de que se trata de uma hipérbole.

Examinando a curva em sua posição original percebemos que seus vértices estão nos pontos (1,1) e (-1,-1), e que os dois ramos tendem aos dois eixos cartesianos.

Observamos também que os focos F₁ e F₂ procurados têm de ser da forma (p,p) e (-p,-p), pois eles pertencem à reta que contem os vértices.

Assim, para mostrar que realmente se trata de uma hipérbole, precisamos:

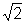i) encontrar dois pontos F₁ e F₂ que sejam os focos, isto é, tais que (*), sendo 2a=2 , para todo ponto 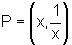da curva;

ii) mostrar que todo ponto (x,y) que verifica a relação (*) é da form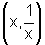a , ou seja, sua ordenada é o inverso da abscissa.

Os cálculos algébricos são bastante trabalhosos, a fim de concluir que vale i) e, para a parte ii) o tratamento algébrico é semelhante.