Os focos estão nos pontos F₁=(m,m) e F₂=(-m,-m), sendo m>0.

Logo, a distância focal é



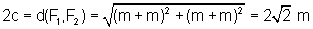
e, portanto, c=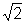 m.

Os vértices estão nos pontos V₁=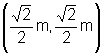 e V₂=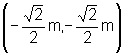

logo, a distância entre eles é dada por:

2a=d(V₁,V₂)=

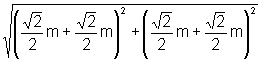
ou seja, 2a=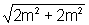

2a=2m

e, portanto,

a=m.

O centro da curva procurada está no ponto (0,0), pois ele é o ponto médio do segmento que tem extremidades nos vértices.

Agora, utilizando a relação entre os parâmetros da hipérbole, temos:

b²=c²-a²

ou seja,

b²= 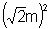-m²=m²

Logo b=m

A equação que descreve a hipérbole procurada, na dependência de m, é:

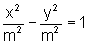
ou seja:

x²-y²=m².