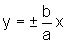Como as assíntotas foram dadas, temos o valor do quociente . De fato, de modo geral, as assíntotas são dadas por , quando o centro da hipérbole está na origem.

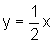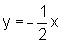Então, como e , temos

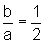, ou seja, a=2b.

Por outro lado, a distância focal 2c=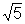 , de onde temos c= .

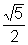Assim, utilizando a relação estabelecida entre os parâmetros que definem a hipérbole, temos:

c²=a²+b²

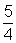=4b²+b²

5b²=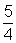

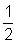b²= , ou seja, b= e, portanto, a=1.

A equação de uma das hipérboles é:

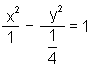
ou seja x² - 4y² = 1

e a equação da outra é:

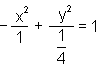
ou seja 4y² - x² = 1